Com simplificar expressions matemàtiques

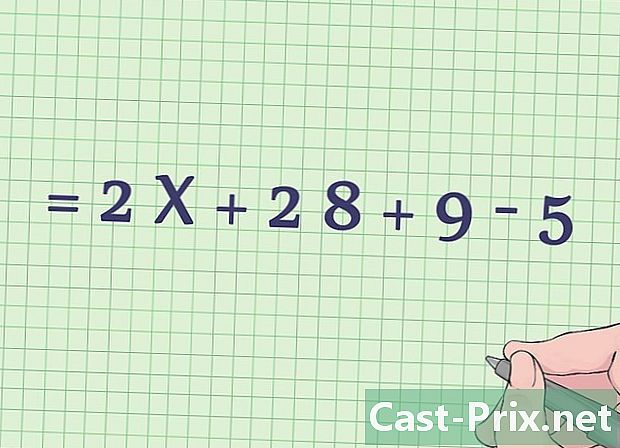
Content

• etapes
• Mètode 1 Respecteu l’ordre de les operacions
• Mètode 2 Simplifiqueu expressions més complexes

Sovint se'ls demana als estudiants que redueixin les expressions matemàtiques "a la seva forma més simple", és a dir, que ho simplifiquin el màxim possible. Tot el que sigui brut o simplificat, l’expressió segueix sent la mateixa, simplement en el segon cas, és més elegant i sobretot més fàcil de manejar. De vegades, l'exercici es considera "acabat" quan l'expressió es redueix a la seva expressió més simple. Per això és important saber com reduir una expressió matemàtica. De fet, és fins i tot una operació gairebé constant. Però continua llegint!

etapes

Mètode 1 Respecteu l’ordre de les operacions

1. 
   

   
   Conèixer l’ordre d’operacions. Quan hom vol simplificar una expressió matemàtica, no funciona idioticament d’esquerra a dreta, segons el que es presenta. Algunes operacions tenen prioritat respecte a d’altres i s’han de fer primer. Si no seguiu aquest ordre, no obtindreu el resultat adequat. L’ordre d’operacions és: parèntesis, exponents, multiplicació, divisió, suma i finalment resta. És un mitjà mnemònic per mantenir aquest ordre: penseu en "PEMDAS": "Perquè diu Ma: Espereu Simone!" (gratuït per trobar-vos millor!)
   • És bo conèixer aquest ordre i és útil per a moltes expressions, però a vegades cal que es simplifiquin tècniques més complexes, inclosos els polinomis. Vegeu el mètode dos per obtenir més informació.

2. 
   

   
   
   
   Comença per tractar el que hi ha entre parèntesis. En matemàtiques, hi ha per indicar que el seu contingut té prioritat sobre qualsevol altre element. Aquesta prioritat és vàlida independentment de les operacions de dins. D’altra banda, però és lògic, dins dels parèntesis, s’aplica l’ordre de les operacions. Així, primer hem de fer les multiplicacions, després les addicions, etc.
   • Per exemple, utilitzarem l’expressió: 2x + 4 (5 + 2) + 3 - (3 + 4/2). Primer cal calcular-ho tot entre parèntesis. 5 + 2 i 3 + 4/2, que ens dóna 5 + 2 = 7 i 3 + 4/2 = 3 + 2 = 5.
     • El segon terme entre parèntesis dóna 5 perquè, primer, si seguim l’ordre d’operacions, dividim 4 per 2. Si agafem el terme tal com ve a l’ordre, fem 3 + 4 i dividim per 2, és a dir per dir que aconseguim 7/2: or, està malament!
   • Nota bene : si hi ha un parèntesi al parèntesi, comencem sempre per la de dins i acabem amb la de fora.

3. 
   

   
   
   
   Després anem als expositors. Ara que hem tractat els parèntesis, hem d’atacar els exponents (si n’hi ha, per descomptat!) Un nombre amb un exponent és fàcil de detectar: ​​hi ha un número (base) i a la part superior dreta, escrit en més petit , l’exponent, també un número. Feu els càlculs per separat i, a continuació, substituïu el valor per exponent pel seu valor calculat.
   • Ara que hem tractat els parèntesis, la nostra expressió és ara: 2x + 4 (7) + 3 - 5. L’únic terme amb exponent aquí és: 3, que és igual 9. Substituïm l'expressió i obtenim: 2x + 4 (7) + 9 - 5.

4. 
   

   
   És el torn de les multiplicacions! Ara, s’han de realitzar totes les operacions de multiplicació. El signe de la multiplicació ve de diferents formes: el símbol ×, un punt, un asterisc o, fins i tot, res! per tant, 4 (i) és una multiplicació, és l’equivalent a 4 x y
   • Hi ha dues multiplicacions en el nostre exercici: 2x (2x = 2 × x) i 4 (7). Com que no coneixem el valor de x, deixem el terme tal com és, però, 4 (7) = 4 × 7 = 28. L’equació es converteix llavors: 2x + 28 + 9 - 5.

5. 
   

   
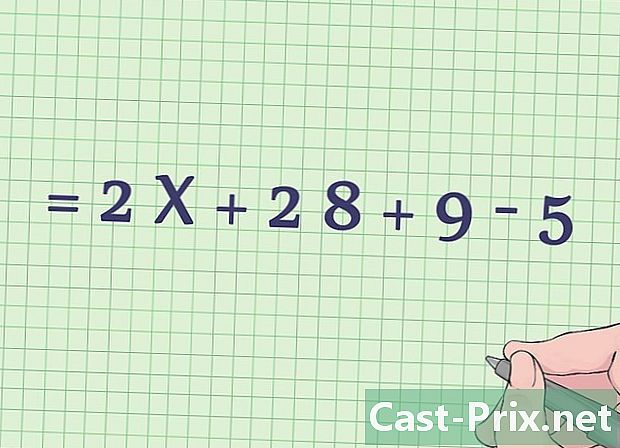
   Passem a la divisió. Igual que el signe de multiplicació, el signe de divisió es presenta de diferents formes: el símbol ÷, però també la barra (/ o "barra", com en 3/4, per exemple - i la línia de fracció horitzontal.
   • En el nostre exemple, no hi ha divisió (excepte els 4/2 vistos més amunt), així que omitirem aquest pas. Aquesta observació requereix un comentari: apliquem el principi PEMDAS en la mesura que l'operació existeixi a la vostra expressió, en cas contrari passem a la següent operació.

6. 
   

   
   A continuació, afegiu-hi. El següent pas és afegir-ho tot. Per descomptat, podem afegir d'esquerra a dreta, però de vegades podem fer agrupacions. Per exemple, amb l’expressió 49 + 29 + 51 + 71, és millor fer 49 + 51 = 100 i 29 + 71 = 100, que dóna: 100 + 100 = 200, en lloc de 49 + 29 = 78,78 + 51 = 129, i 129 + 71 = 200.
   • Com a resultat de les operacions PEMD, la nostra expressió sembla: "2x + 28 + 9 - 5". Ara hem d’afegir el que hauria de ser: agafem els afegits ja que vénen d’esquerra a dreta. No es pot afegir 2x i 28, perquè hi ha una variable (x no es pot afegir fins que no coneguis el seu valor numèric). Pel que fa al 28 + 9, això dóna 37. Si tornem a escriure l'expressió, tenim: "2x + 37 - 5".

7. 
   

   
   Restar. El darrer pas de PEMDAS és la resta. Només haureu de restar restes (però això no és obligatori). Aquest pas s’hauria pogut fer prèviament si considerem que restar és sumar un nombre negatiu. Aquestes dues últimes operacions (suma i resta) són intercanviables.
   • Gràcies a PEMDA, la nostra expressió sembla: "2x + 37 - 5". Ara restarem el que podem. Podem restar 5 de 32, que és 32 - 5 = 32.

8. 
   

   
   Comproveu la vostra expressió per última vegada. Normalment, en aquest moment, la vostra expressió es redueix al màxim. En el cas particular d'equacions amb un desconegut (x), teniu una expressió reduïda, però no del tot. Serà quan x s'assigna un valor numèric. Tot i això, també és possible simplificar una equació amb incògnites (vegeu més avall).
   • S'ha tingut en compte tot PEMDAS, la resposta final és: "2x + 32". No es pot simplificar més, perquè no es poden afegir 32 i 2x per la presència d’una variable, 2x. Quan coneixem el valor de x, podrem acabar els càlculs. Reconeix que encara és més pràctic que l’expressió original! expressió.

Mètode 2 Simplifiqueu expressions més complexes

1. 
   

   
   Afegiu les incògnites idèntiques. Si teniu una incògnita en la vostra expressió, sabeu que podeu afegir o restar incògnites idèntiques amb el mateix exponent (o "termes idèntics"): funciona exactament amb nombres normals. Repetim-ho: el desconegut ha de ser idèntic i l’exponent també! Per exemple, 7x i 5x es poden afegir, però no 7x i 5x.
   • Aquesta regla també s'aplica als termes que contenen múltiples incògnites. Per exemple, 2xy es pot afegir a -3xy, però no a -3xy o -3y.
   • Mirem de prop l’expressió: x + 3x + 6 - 8x. Aquí podem afegir 3x i -8x perquè tenen la mateixa potència. Simplificada, l'expressió es converteix en: x - 5x + 6.

2. 
   

   
   Simplifiqueu una fracció dividint o suprimint "factors comuns". Les fraccions que només inclouen valors numèrics (absència d'incògnites), tant del numerador com del denominador, poden simplificar-se de diferents maneres. Primer (potser el més senzill) mètode: dividiu el numerador directament pel denominador. A més, si teniu un producte a la part superior i inferior de la fracció i un dels termes apareix a banda i banda, podeu "simplificar" perquè anul·len (la seva divisió és igual a 1). Per tant, per resumir, si tots dos termes estan presents per sobre i per sota de la barra de fraccions, podeu suprimir els dos.
   • Per exemple, prenem la fracció 36/60. Si teniu una calculadora, feu la divisió directament, el resultat serà: 0,6. Si no en teniu, podeu suprimir els factors comuns. Per fer-ho, desgloseu els dos nombres en factors i vegeu si hi ha algun factor comú. 36/60 = (6 × 6) / (6 × 10), o si preferiu: 6/6 × 6/10. Com que 6/6 és igual a 1, l'expressió es converteix en 1 × 6/10 = 6/10. No està completament acabat, ja que 6 i 10 són divisibles per 2, obtenim 3/5o 0,6.

3. 
   

   
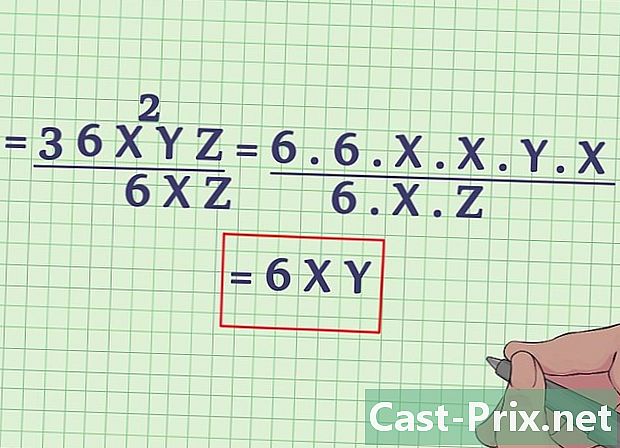
   Per a fraccions amb incògnites, és el mateix. Mireu si no hi ha termes (amb una incògnita) comuns a les dues parts de la fracció. Podem simplificar la incògnita amb el seu coeficient i exponent.
   • Prenguem l’expressió (3x + 3x) / (- 3x + 15x). Aquesta fracció es pot escriure de la forma: (x + 1) (3x) / (3x) (5 - x), 3x apareix tant al numerador com al denominador, de manera que podem eliminar-lo a la part superior i inferior. A continuació, obtenim: (x + 1) / (5 - x). De la mateixa manera, a l'expressió (2x + 4x + 6) / 2, tots els termes són divisibles per 2. Obtenim llavors: (2 (x + 2x + 3)) / 2, i més: x + 2x + 3.
   • Atenció! aquesta simplificació només funciona si es té un producte de factors a la part superior i es detta a la part inferior. Per exemple, a l’expressió (x (x + 2)) / x, podem simplificar-ho per “x”, que ens dóna: (x + 2) / 1 = (x + 2). En canvi, amb (x + 2) / x, no podem fer res perquè tenim una suma a la part superior i no un producte. No es pot simplificar en aquesta forma: 2/1 = 2.

4. 
   

   
   Desenvolupar o factoriar? En alguns casos, quan volem simplificar, per estrany que sembli, és millor desenvolupar que factoritzar. No hi ha cap norma establerta. Només amb l’hàbit que veiem què s’ha de fer, l’objectiu sempre és simplificar l’expressió.
   • Per exemple, l'expressió 3 (x + 8), quan s'expandeix, proporciona: 3x + 24, mentre 3x + 24x es pot fer en consideració, i donarà: 3x (x + 8).
   • En alguns casos, és millor mantenir el factor constant davant d’una expressió entre parèntesis. De fet, es pot portar a desaparèixer. És inútil desenvolupar-nos massa aviat, la simplificació sempre és possible. A la fracció (3 (x + 8)) / 3x, per exemple, 3 està present en el numerador i el denominador, de manera que podem suprimir-lo, que dóna: (x + 8) / x. Encara és més fàcil de manejar que (3x + 24x) / 3x, el resultat que hauríem obtingut si ho haguéssim desenvolupat tot.

5. 
   

   
   Simplifiqueu el factoring. Factoring és una tècnica que pot simplificar una fracció eliminant de vegades polinomis. El factoring és el contrari al desenvolupament. Una expressió llarga, una suma en general, es transforma en una expressió més curta que és producte de factors. Aquesta factorització només s’ha de fer si, al darrere, hi ha simplificació (com en una fracció). En alguns casos (sovint amb equacions de segon grau), el factoring també permet trobar les arrels de l’equació més ràpidament i fàcilment.
   • Reprenguem l’expressió x - 5x + 6. Aquesta expressió es pot considerar en (x - 3) (x - 2). De manera que, si més endavant, x - 5x + 6 es troba en el numerador d’una fracció, i si tinguéssim (x - 2) en denominador, podríem simplificar aquest terme. Exemple: hem de simplificar (x - 5x + 6) / (2 (x - 2)). Primer factoritzem el numerador i, després, simplifiquem. En altres paraules, acabem amb (x - 3) (x - 2) / (2 (x - 2)), simplifiquem per (x - 2) i obtenim: (x - 3) / 2.
   • Com s'ha apuntat anteriorment, hi ha de vegades altres motius de factorització.En efecte, aquesta manipulació serveix per simplificar, però també permet resoldre més fàcilment una equació, sobretot si aquesta última és igual a 0. Per exemple, agafem l’equació x - 5x + 6 = 0. Si es factoritza, s’obté: x - 3) (x - 2) = 0. Per resoldre aquesta equació, n’hi ha prou que un dels termes sigui igual a 0, ja que 0 vegades x = 0. Per tant, 3 i 2 són les solucions.